Проф. Николай Янев: Как ще се развие епидемията за следващите няколко дни

Проф. Николай Янев е ръководител на авторски колектив от математици от БАН, СУ и НБУ, които създадоха математичен модел за анализ на епидемията от COVID-19, основаващ се на разклоняващи се стохастични процеси. Моделът вече се ползва в цял свят от учените, които могат да прогнозират епидемията във всяка страна, където има статистика за броя на заразените, новозаразените, клинично проявените случаи и пр. Моделът и съответният софтуер са създадени за около месец по повод скоростното развитие на епидемията в Италия.

Проф. дмн Янев  представи 5-дневна прогноза за развитието на епидемията у нас:

Нашият модел ползва данни от официалната статистика на СЗО, които всеки ден се акумулират в него за всяка една страна. От математическа гледна точка той е сравнително прост, но има голямо преимущество пред други, по-сложни модели, защото дава информация за най-важния епидемиологичен параметър m, а именно колко души средно може да зарази един индивид от първи тип. Така наричаме един „ненаблюдаем“ или неизвестен заразоносител, човек, който разнася заразата, без да подозира това. За тази цел се използват само официални данни за втория тип индивид, това е човек, вече идентифициран като заразоносител (позитивен). Така прогнозираме средния брой на „неосветените“ индивиди M, които играят основна роля в разпространението на вируса.

Например, за България се оказва, че един заразен, но „неосветен“ индивид, може да зарази средно на ден m=1.1093 души, а в Италия – m=1.1348. Разликата в двете числа на пръв поглед изглежда  несъществена, но на практика става въпрос за това, че в Италия един човек може да зарази много повече хора, като се има предвид, че броят на заразените нараства експоненциално. С този параметър m може да обясни защо епидемията в Италия се разви с такава смайваща скорост.

Тук трябва да отбележа, че тя започна преди доста време и там има данни за много по-дълъг период, тоест m би трябвало да е по-точно.  По принцип графиките, които правим, имат три оценки и според тях – има три вида сценария. Тези оценки определят каква ще бъде динамиката на епидемията – ще затихва, ще се развива или ще е константна. В Германия обявиха, че тъй като m e по-малък от 1, те решили да разхлабят мерките. И аз си помислих, че вероятно са ползвали нашия модел и един от нашите сценарии. Той е отворен за целия свят и всеки, който разбира от статистика, може да влезе и да го ползва.

Има страни в  света, чиито показател m е по-нисък от този в България и в Италия, тоест, там един човек заразява по-малко хора, но трябва да се вземе предвид фактът, че една част от тях нямат или не съобщават верни данни за епидемията.

Ние не работим с хипотези, а използваме преди всичко дадените статистики. Въпросът е доколко те са репрезентативни. Защото в някои страни има много повече наблюдения и статистиките са много адекватни, в други страни – те са по-малко и извадката не е толкова репрезентативна.

Ако данните не са репрезентативни, то и пресмятанията не са адекватни. В някои страни броят на индивидите от втори тип (т.е. официално регистрираните заразени) не е голям, тъй като бързи тестове не се правят или пък се правят много малко. Затова можем да кажем, че колкото повече данни има за разпространението на вируса сред популацията, толкова по-точна ще бъде прогнозата.

Като това трябва да е съотносително с популацията, която се изследва. Например за САЩ тази извадка трябва да бъде много голяма, защото те са 333 млн. души, а за България, която е 7 млн., извадката трябва да бъде около 47 пъти по-малко. Колко точно – не може да се каже без специално допълнително проучване. Да се вземат тестове от случайно избрани хора, от различни групи в обществото, от рискови групи. Тоест, да се направи малък обхват на цялата популация, дори не знам дали някъде въобще правят такова нещо в пълен обем. Но по принцип е добре да се почне от рисковите групи и колкото повече хора се обхванат, толкова по-добре.

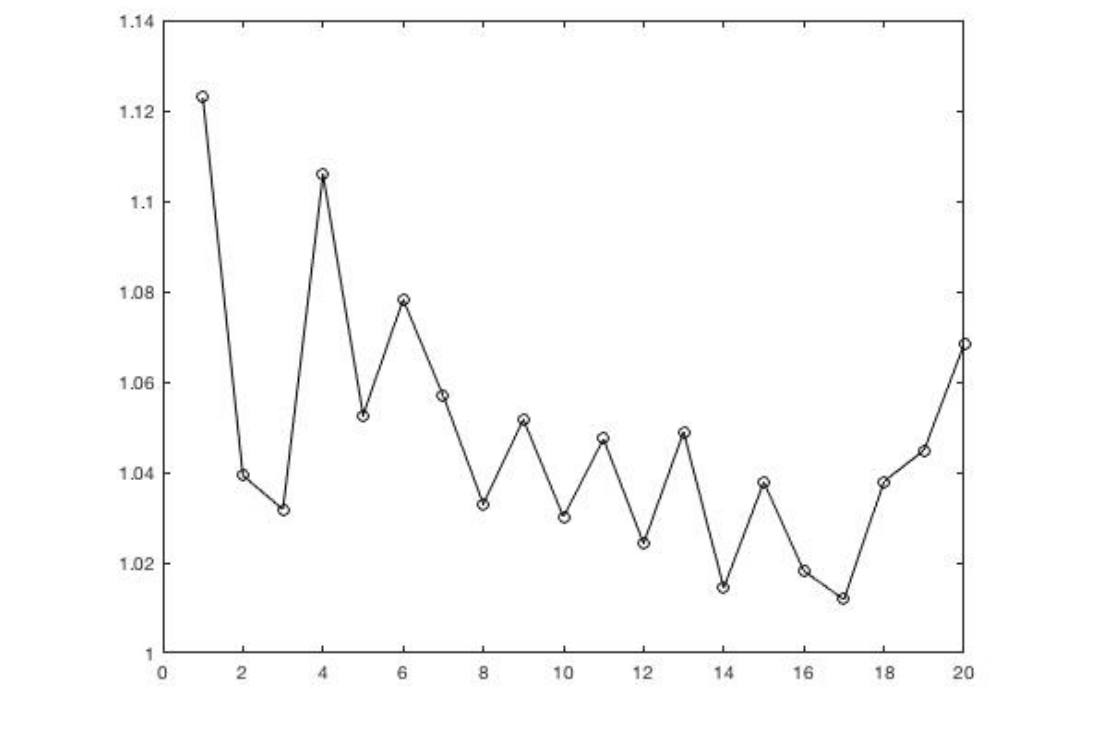
Пред Клуб Z  проф Янев направи  следната прогноза: На графика 1 се вижда как намалява числото m за последните 20 дни – 29 март-17 април, вследствие на наложената карантина стига почти до 1. Но през последните 3 дни започва отново да се катери нагоре към 1.06.

Изменение на оценката за репродукция на процеса за 20 дни (29 март – 17 април).

Въз основа на числото m може да се пресметне колко души M, за които никой няма идея, ще се заразят. Вижда се, че техният брой се увеличава плавно и от 116 души на 18 април, ще стигне 151 души на 23 април.

С други думи, ако Щабът каже, че са установени 20 новозаразени, той говори за откритите новозаразени, а с нашия модел ние прогнозираме колко са новозаразените, които са в сянка. Те са няколко пъти повече. Това е едно от достойнствата на модела.

Съотношението между всички заразени и клинично доказаните болни също се мени всеки ден, но към момента α = 0.3279, което означава, че една трета от заразените се регистрират с някакви оплаквания или са открити с тестове.

Трябва да се обърне внимание, че всички тези оценки са дадени с 95% доверителни интервали. Това означава, че в 95% от случаите ще познаем, че съответните стойности са именно в този интервал, но в 5% от случаите можем и да не познаем.

Това е така, защото изследваните явления имат стохастичен, т.е. случаен характер. И това е една от особеностите на този феномен. Всъщност с вероятност 0.95 е възможно да се наблюдава всяко едно от числата в този интервал. А посочените оценки са просто средите на тези интервали, но това не ги прави в никакъв случай по-вероятни от другите стойности в интервала. В нашия модел конструирането на тези доверителни интервали е сложна математичска задача. А въобще математическата статистика борави винаги с доверителни интервали и ако в някои статистически изследвания те липсват, то това поставя под съмнение всички изводи след това.

За българите, завърнали се от чужбина Не знаем официалните данни, но някои медии съобщиха, че са се върнали около 200 000 имигранти. Някои от тях се концентрират в условно да ги наречем, имиграционни депа. По отношение на нашия модел наличието на такава допълнителна имиграция коренно променя развитието на епидемията в нашата популация. И вече имаме два различни модела.

Освен това, в тези депа влизат постоянно нови имигранти, а много излизат от тях, тоест има последваща имиграционна вълна, и този процес може да не затихва, а да се развива вълнообразно.

Ето защо ние разширихме нашия първоначален модел и сега подготвяме втора публикация, където се отчита същественото влияние на имиграцията. При това се очертават четири възможни сценария, зависещи основно от параметъра на средно заразяване, който означихме по-горе с m.

Така, ако m>1, то имаме експоненциален ръст на популацията от заразени (независимо дали моделът е без или с имиграция). Ако m=1 (или варира близо до 1), то при модела без имиграция средният брой заразени е постоянен, докато при модела с имиграция средният брой заразени расте линейно. При m<1 процесът без имиграция затихва, т.е. инфекцията намалява и клони към нула, но при наличие на имиграционна компонента средният брой заразени  не намалява, а остава константен. В този последен случай може да се каже, че инфекцията, грубо казано, продължава да тлее.

Във връзка с това смятам, че у нас се вземат адекватни мерки, въпреки че някои ги оценяват като прекалено строги. Напротив, както се вижда от въпросните сценарии, тези мерки може би трябва да бъдат още по-рестриктивни.

Трудно могат да се направят, защото нямаме аналози на тази епидемия, много неща не се знаят, епидемиолозите непрекъснато се тюхкат, а те трябва да дадат тази информация на нас, математиците.

Нашият модел използва само това, което се наблюдава и колеги от други страни оцениха точно това, че с един сравнително по-прост модел може да се получи най-важната информация. Той, така да се каже, дава един бърз, но ефикасен тест за оценяване скоростта на заразяване.

Разбира се, има нужда от по-сложни епидемиологични модели. Но те изискват време и сериозна колаборация между епидемиолози, математици, медици, информатици, микробиолози, молекулярни биолози и други специалисти заедно с използване на натрупаната сериозна научна информация по този проблем.